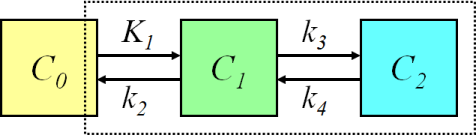
Workable model

All reliable information about the transport and biochemical reactions of the tracer must be incorporated in the comprehensive model. As a consequence, comprehensive model consists of many separable pools (compartments). The mathematical complexity increases drastically as the number of compartments becomes large. Analytical solutions for models of more than three compartments are possible only in rare cases. A model needs to be reduced to become a useful tracer kinetic model, which provides identifiable parameter values. Alternatively, experimental protocol must be expanded to collect more information (Delforge et al., 1989). Methods for assessing structural and numerical model identifiability have been reviewed specifically for PET by Roger Gunn in his thesis, and more generally in the book Identifiability of Parametric Models.

However, it should be kept in mind that simplicity is no proof of validity and that validity is not necessary a prerequisite to utility (Garfinkel, 1980).

Reducing the model

There are several approaches to reduce the complexity of a model by using the quantitative information of physiology and biochemistry:

Combining adjacent compartments

If the relative magnitudes of a series of transport steps or reactions are known, the limiting (slower) steps can be identified. Separate compartments can then be combined to form a single compartment if the transport rates between them are not limiting.

Common examples:

In the brain tissue the transport across the cell membrane is assumed to be much faster than the transport across the capillary wall; concentration ratio between the interstitial space and the intracellular space is nearly in equilibrium at all times. Therefore these compartments can be approximated as a single compartment.
With ligand-receptor models, a common assumption is that the binding and release of ligand from nonspecific binding sites is not a limiting step (k₅ & k₆ ≫ k₃ & k₄), and the compartments of nonspecifically bound and free ligand in tissue can be combined into one.

Effect of perfusion

If the delivery of the tracer is high compared to the extraction (PS value is small compared with perfusion), so that the plasma concentration of tracer along the capillary does not vary much, the transport of tracer into tissue is almost independent of perfusion. In such a case the model can be further simplified by eliminating the effect of blood flow. For example, in the brain, the FDG model could be reduced to this configuration:

, where the first compartment represents the concentration of FDG in arterial plasma, the second compartment represents the concentration of FDG in the brain region, and the third compartment represents the concentration of phosphorylated FDG in the brain region.

In peripheral organs the endothelial barrier may not be limiting factor for the kinetics of radiopharmaceutical like the blood-brain barrier in central nervous system. Then it may be possible to simplify the model by combining the compartments for the vascular and interstitial space. Unfortunately, the perfusion and permeability of endothelial barrier in peripheral organs may be very variable.

Constraining parameters

Another approach to reduce the complexity of a model and to resolve the non-uniqueness problem is to assign parameter to a known or fixed value.

Although the mathematical complexity of the model solution is not reduced, the parameter estimation problem is improved. Simpler models are more tolerant of noise and require less detailed data than more complex models, if the goal is to determine all the parameters in the more complex model. A more realistic model with some parameters pre-established at reasonable levels is more accurate than a less realistic model that ignores those parameters altogether (Graham, 1985).

Constraining ("fixing") the distribution volume (K₁/k₂) for ¹⁵O labeled water for a literature value, or assigning an independently measured value for vascular fraction in tissue, are examples of this approach. In brain receptor studies, an estimate of K₁/k₂ in receptor-free area can sometimes be assigned for other regions.

If the assigned values of the parameters differ from the true values of a particular study, the deviation can be reflected as systematic errors in other parameters. Sometimes a trade-off has to be made: which are more useful, parameter estimates with bias or with large variability.

A good example of practical model development for a PET radiotracer with very complex kinetics is the articles by Mankoff et al (1998 and 1999).

Physical interpretation of model parameters

The physical meaning of the model parameters is changed when the number of compartments in a model is reduced. When two compartments are combined to one, the rate constants for transport out of the new compartment refer to the total amount of tracer in the new compartment. This change must be considered when assigning constrained (fixed) values to parameters, validating the model, or interpreting model predictions.

The value of a rate constant in a compartmental model is different from the physical of chemical rate constants. Since the rate constant in compartmental model is with respect to the amount of tracer in a compartment, it is related to both the tracer concentration and the volume of the space that the compartment represents. The term distribution volume (V_T or V_d) is frequently used in tracer kinetics; it is the volume of tissue space in which the tracer would have distributed with the same concentration as in blood. It is defined mathematically as the equilibrium ratio of the concentration of tracer in tissue to the concentration of tracer in blood, and is identical to the term partition coefficient, p.

Receptor model for the brain can often be reduced to a similar model than with FDG. After combining the compartments for nonspecific binding and free ligand, the physical meaning of partition coefficient changes, and the actual value can be very different from the expected value (usually near unity). The nonspecific binding to plasma proteins is usually ignored, which also changes the partition coefficient. In receptor model with tracer concentrations the parameters k₃ and k₄ can be defined with terms of receptor binding (Mintun et al., 1984).

Macroparameter

Combination of model parameters can be computed with better reproducibility from lesser data than the separate rate constants. "Macroparameter" is calculated either by combining the individually estimated compartmental model parameters, or, applying a specific analysis method that directly computes an estimate of the macroparameter.

Commonly used macroparameters net influx rate (K_i) for irreversible tracer uptake and total volume of distribution (V_T) and binding potentials as its derivatives for reversible tracer uptake can be calculated from compartmental model parameters or using graphical analysis methods.

Compartmental model parameter k₃ is often measured as a perfusion and plasma protein binding independent index of enzyme activity in the brain. Reliable estimation of k₃ is difficult if k₃ >> k₂. A macroparameter λ*k₃ (where λ=K₁/k₂) can be calculated as an alternative, which is independent of perfusion and nonspecific binding in tissue, but is dependent on plasma protein binding (Fowler et al., 1999; Logan et al., 2002). The λ*k₃ can be calculated from compartmental model parameters, or from equation

\[ \lambda k_3 = \frac{K_1 K_i}{K_1 - K_i} \]

In the case of reversible binding, the ratio of plasma input compartmental model parameters k₂ and k₃ is often assumed to represent binding potential. However, in some cases k₂/k₃ cannot be reliably determined, and V_T can be shown to correlate better with the protein concentration (Zanotti-Fregonara and Bottlaender, 2014).

Literature

Budinger TF, Huesman RH, Knittel B, Friedland RP, Derenzo SE. Physiological modeling of dynamic measurements of metabolism using positron emission tomography. In: Greitz T et al. The metabolism of the human brain studied with positron emission tomography. Raven Press, New York, 1985. ISBN 0-88167-056-1.

Carson RE. The development and application of mathematical models in nuclear medicine. J Nucl Med. 1991; 32:2206-2208. PMID: 1744704.

Coxson PG, Huesman RH, Borland L. Consequences of using a simplified kinetic model for dynamic PET data. J Nucl Med. 1997; 38: 660-667. PMID: 9098221.

Delforge J, Syrota A, Mazoyer BM. Identifiability and error minimization in estimation of receptor model parameters with PET. In: Positron Emission Tomography in Clinical Research and Clinical Diagnosis: Tracer Modelling and Radioreceptors, edited by C Beckers et al., 1989, 45-64. ISBN 978-0-7923-0254-4.

Garfinkel D. Computer modeling, complex biological systems, and their simplifications. Am J Physiol. 1980; 239: R1-R6. doi: 10.1152/ajpregu.1980.239.1.R1.

Graham MM. Model simplification: complexity versus reduction. Circulation 1985; 72: IV63-IV68. PMID: 4053329.

Gunn R (1996). Mathematical modelling and identifiability applied to positron emission tomography data. PhD thesis, University of Warwick.

Huesman RH, Coxson PG. Consolidation of common parameters from multiple fits in dynamic PET data analysis. IEEE Trans Med Imaging 1997; 16(5): 675-683. doi: 10.1109/42.640758.

Lammertsma AA. Forward to the past: the case for quantitative PET imaging. J Nucl Med. 2017; 58(7): 1019-1024. doi: 10.2967/jnumed.116.188029.

Logan J, Alexoff D, Kriplani A. Simplifications in analyzing positron emission tomography data: effects on outcome measures. Nucl Med Biol. 2007; 34: 743-756. doi: 10.1016/j.nucmedbio.2007.06.003.

Mintun MA, Raichle ME, Kilbourn MR, Wooten GF, Welch MJ. A quantitative model for the in vivo assessment of drug binding sites with positron emission tomography. Ann Neurol. 1984; 15: 217-227. doi: 10.1002/ana.410150302.

Patlak CS, Blasberg RG. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. Generalizations. J Cereb Blood Flow Metab. 1985; 5:584-590. doi: 10.1038/jcbfm.1985.87.

Phair RD. Development of kinetic models in the nonlinear world of molecular cell biology. Metabolism 1997; 46:1489-1495. doi: 10.1016/S0026-0495(97)90154-2.

Schmidt KC, Turkheimer FE. Kinetic modeling in positron emission tomography. Q J Nucl Med. 2002; 46: 70-85. PMID: 12072847.

Tags: Modeling, Macroparameter, Compartmental model

Updated at: 2022-04-04
Created at: 2011-11-22
Written by: Vesa Oikonen