Net influx rate (Ki)
Ki is the unidirectional uptake rate constant that incorporates both net inward transport and trapping of the radiotracer in tissue.
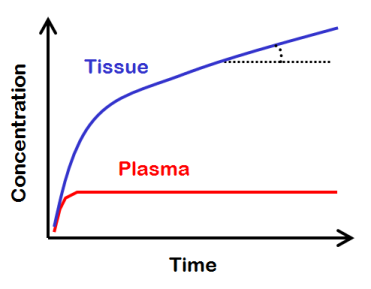
Lets imagine a theoretical situation, where we keep the concentration of radioligand in plasma at a steady level for a very long time.
After some time has passed, radiotracer concentrations in all reversible tissue compartments will reach a dynamic equilibrium with each other and with plasma. Meanwhile the total tissue concentration will continue to increase because of the irreversible process.
The total tissue concentration will increase linearly, with a slope that gives the net influx rate, Ki = slope/plasma. If there were no irreversible process, then tissue curve would reach a steady level, representing the total distribution volume, VT = tissue/plasma.
In bolus infusion PET studies, calculation of Ki is possible when input function is measured from the administration time (0-time) to the end time of the PET scan. Ki can be calculated with compartmental model fitting or multiple-time graphical analysis for irreversible uptake (Patlak plot). Calculation can be done for regional tissue time-activity curves to get regional Ki values, or for dynamic PET images to get parametric Ki image for further analysis. Instead of a full dynamic PET scan, if certain assumptions are met, estimation of Ki may be possible from two static late-scans using dual time point method.
While bolus infusion methods are normally applied in PET, steady-state methods can be used, too, to estimate the Ki. Steady-state methods enable monitoring of transient metabolic changes in vivo. These techniques have been applied in [18F]FDG PET in small animals (Bérard et al., 2006) and in human brain activation studies, termed as fPET (Villien et al., 2014).
Ki and compartmental model
Ki is not dependent on compartmental model, although it can also be derived from the differential equations of compartmental models.
Three-tissue compartmental model
Assuming that compartments are in series,
Two-tissue compartmental model
Assuming that k4=0:
One-tissue compartmental model
Assuming that k2=0:
Notice that Ki is partially, and non-linearly, dependent on perfusion (a component of K1 and k2). This may lead to difficulties when perfusion is low compared to the irreversible process that we try to quantitate.
Metabolic rate
When the PET radiopharmaceutical is an analog of glucose (e.g. [18F]FDG) or fatty acids (e.g. [18F]FTHA) or other native substrate in the tissue, and it is metabolically trapped in tissue during the PET scan, Ki can be used to calculate the metabolic rate of the native substrate. For example, in [18F]FDG the Ki can be multiplied by concentration of glucose in plasma, and divided by the appropriate lumped constant, to get an estimate of glucose uptake rate.
LC for [18F]FDG accounts for the differences in transport and phosphorylation rates between glucose and [18F]FDG.
See also:
- Calculation of FUR image
- Calculation of regional FUR
- Standardized Uptake Value (SUV, DUR)
- Patlak plot
- Interpretation of Patlak plot by Lars Jødal
- Dual time point estimation of Ki
- Carimas software
Literature
Allman KC, Stevens MJ, Wieland DM, Hutchins GD, Wolfe ER Jr, Greene DA, Schwaiger M. Noninvasive assessment of cardiac diabetic neuropathy by carbon-11 hydroxyephedrine and positron emission tomography. J Am Coll Cardiol. 1993; 22: 1425-1432. doi: 10.1016/0735-1097(93)90553-D.
Camici P, Araujo LI, Spinks T, Lammertsma AA, Kaski JC, Shea MJ, Selwyn AP, Jones T, Maseri A. Increased uptake of 18F-fluorodeoxyglucose in postischemic myocardium of patients with exercise-induced angina. Circulation 1986; 74(1): 81-88. doi: 10.1161/01.CIR.74.1.81.
Villien M, Wey H-Y, Mandeville JB, Catana C, Polimeni JR, Sander CY, Zürcher NR, Fowler JS, Rosen BR, Hooker JM. Dynamic functional imaging of brain glucose utilization using fPET-FDG. NeuroImage 2014; 100: 192-199. doi: 10.1016/j.neuroimage.2014.06.025.
Tags: Patlak plot, Ki, Macroparameter
Updated at: 2022-10-18
Created at: 2014-01-27
Written by: Vesa Oikonen